CBSE CLASS XII
MATHEMATICS SYLLABUS
TERM-2
(2021-2022)
The Syllabus in the subject of Mathematics has undergone changes from time to time in accordance with growth of the subject and emerging needs of the society. Senior Secondary stage is a launching stage from where the students go either for higher academic education in Mathematics or for professional courses like Engineering, Physical and Biological science, Commerce or Computer Applications. The present revised syllabus has been designed in accordance with National Curriculum Framework 2005 and as per guidelines given in Focus Group on Teaching of Mathematics 2005 which is to meet the emerging needs of all categories of students. Motivating the topics from real-life situations and other subject areas, greater emphasis has been laid on application of various concepts.
OBJECTIVES:
The broad objectives of teaching Mathematics at senior school stage intend to help the students:
- to acquire knowledge and critical understanding, particularly by way of motivation and visualization, of basic concepts, terms, principles, symbols and mastery of underlying processes and
- to feel the flow of reasons while proving a result or solving a
- to apply the knowledge and skills acquired to solve problems and wherever possible, by more than one
- to develop positive attitude to think, analyze and articulate
- to develop interest in the subject by participating in related
- to acquaint students with different aspects of Mathematics used in daily
- to develop an interest in students to study Mathematics as a
- to develop awareness of the need for national integration, protection of environment, observance of small family norms, removal of social barriers, elimination of gender
- to develop reverence and respect towards great Mathematicians for their contributions to the field of Maths.
TERM – II
| No. | Units | Marks |
| III. | Calculus | 18 |
| IV. | Vectors and Three-Dimensional Geometry | 14 |
| VI. | Probability | 8 |
| Total | 40 | |
Unit-III: Calculus
- Integrals
Integration is an inverse process of differentiation. Integration of a variety of functions by substitution, by partial fractions and by parts, Evaluation of simple integrals of the following types and problems based on them.
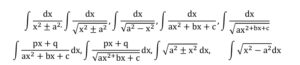
Fundamental Theorem of Calculus (without proof).Basic properties of definite integrals and evaluation of definite integrals.
2. Applications of the Integrals
Applications in finding the area under simple curves, especially lines, parabolas; area of circles /ellipses (in standard form only) (the region should be clearly identifiable).
3. Differential Equations
Definition, order and degree, general and particular solutions of a differential equation. Solution of differential equations by the method of separation of variables, solutions of homogeneous differential.
Unit-IV: Vectors and Three-Dimensional Geometry
- Vectors
Vectors and scalars, magnitude and direction of a vector. Direction cosines and direction ratios of a vector. Types of vectors (equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, the addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Definition, Geometrical Interpretation, properties and application of scalar (dot) product of vectors, vector (cross) product of vectors.
2. Three-dimensional Geometry
Direction cosines and direction ratios of a line joining two points. Cartesian equation and vector equation of a line, coplanar and skew lines, the shortest distance between two lines. Cartesian and vector equation of a plane. Distance of a point from a plane.
Unit-VI: Probability
- Probability
Conditional probability, multiplication theorem on probability, independent events, total probability, Bayes’ theorem, Random variable and its probability distribution.
TO DOWNLOAD THE FULL PDF CLICK THE BELOW LINK:
LINK:
DOWNLOAD MATHS TERM-2 SYLLABUS
Hope you found it useful,
FOLLOW US ON: